Опря В. Р.
Принципы теории относительности и свойства времени
1. Принципы относительности
Теорию относительности часто считают разделом физики, который изучает движение объектов со скоростями сравнимыми со скоростью света. Речь идет не об определениях в учебниках физики, а о восприятии теории относительности. И не только людей, далеких от науки, людей, но, отчасти, и в среде физиков. Но в такой интерпретации получается, что эта теория описывает исключительно некие экстремальные условия, и является частным случаем классической физики. И, в учебниках физики, так эта теория обычно и описывается, вначале дается основа в виде кинематики классической физики, а затем, на этой прочной базе строится теория относительности. Теория относительности действительно исторически выросла из классической физики, но описывает эта теория не только явления, происходящие за пределами физики Ньютона, формулы теории относительности универсальны, и они верны, и в случае быстрого относительного движения тел, и в случае движения тел со скоростями значительно меньшими, чем скорость света. Таким образом, именно кинематика классической физики является частным случаем теории относительности, а не наоборот. И пусть, явления классической физики лучше изучены и более наглядны, просто потому, что их можно наблюдать непосредственно, именно теория относительности является базисом, на физических и философских принципах которого должна строиться и релятивистская и классическая физика. Таким образом, теория относительности, прежде всего, изучает основополагающие вещи, свойства пространства, и свойства времени, а уже затем, явления связанные с перемещением в пространстве. Вот с этой точки зрения, я предлагаю проанализировать связь принципов относительности, сформулированных Эйнштейном, и физических свойств времени. Общеизвестно, что в основе теории относительности лежат два принципа, но для построения теории, только этих принципов недостаточно даже для построения специальной теории относительности, а для построения общей теории относительности были введены дополнительно еще три принципа [1 стр. 613]. Но значимость первых двух принципов, сформулированных в 1905 году, и немного отредактированных позже, действительно безусловна. Первый принцип относительности Эйнштейна фактически повторяет принцип относительности Галилея, который сформулировал независимость законов механики от выбора инерциальных систем отсчета. Смысл принципа относительности в редакции Эйнштейна состоял в том, что этот принцип верен и в случае скоростей сравнимых со скоростью света в вакууме. А второй принцип относительности распространял эквивалентность законов физики также и на явления электродинамики Максвелла, то есть утверждал, что в любой инерциальной системе отсчета скорость света одинакова. В образной форме, первый принцип относительности можно описать на примере нескольких физиков, попавших в затруднительную ситуацию. Проснувшись, несколько физиков обнаруживают себя в неком замкнутом пространстве, в котором на них не действует сила тяжести, и они просто висят в невесомости. Здорово! Вот только понять бы, где они оказались. Первый из физиков высказывает предположение, что по ошибке они очутились в экспериментальной установке, в которой экранируют гравитацию Земли. Но ему возражают его приятели, что они физики, и знают, что на Земле таких установок еще нет. Поэтому второй физик предлагает другую версию, что они оказались на борту космического корабля, который свободно движется без ускорения по орбите Земли. Третий физик возражает. Он говорит: "Нет, ну что вы! Кому придет в голову выкинуть несколько миллионов, чтобы запустить нас в космос? Это фантастика, такого просто не может быть. Скорее всего, нас похитили инопланетяне и мы теперь со скоростью, близкой к скорости света движемся к какой-нибудь далекой звезде". Ну и вот, по поводу двух последних версий, между физиками завязался спор, какая из них фантастична, а какая более правдоподобна. И решить бы этот спор экспериментально, но дело только в том, что, согласно принципам относительности Эйнштейна, экспериментально решить этот спор невозможно. Теория относительности построена на ряде постулатов и основной постулат, принцип относительности Эйнштейна, гласит, что все инерциальные системы отсчета совершенно равноправны и все законы природы во всех инерциальных системах отсчета одинаковы, и в первую очередь, это касается хода времени и скорости света. "Законы природы не зависят от состояния движения системы отсчета, по крайней мере, если она не ускорена". ([1] стр. 69) И, если появившаяся немного раньше теория эфира Лоренца просто предполагала существование ряда эффектов, таких как изменение длины тел, в направлении движения, замедление хода времени и увеличение массы движущегося тела, из-за которых определить настоящую неподвижную систему отсчета было затруднительно, то, согласно предположению Эйнштейна, любые две инерциальные системы отсчета эквивалентны. То, есть, что никакой выделенной "настоящей" неподвижной системы отсчета не существует в принципе. В литературе, посвященной теории относительности часто можно найти утверждения о том, что с объектом, движущимся относительно наблюдателя с большой скоростью, происходят некоторые необычные явления, такие, как замедление хода времени, сокращение размеров в направлении движения и увеличение массы. И все эти эффекты преподносятся как следствия теории относительности. На самом деле, в этой области большая путаница, которая появилась в результате смешивания классических методик наблюдения с новыми представлениями о мире. Показательной в этом смысле, является очень часто встречающиеся в литературе по теории относительности утверждения о том, что при увеличении скорости, увеличивается и масса тела. Эта концепция появилась еще до теории относительности и была введена именно для того, чтобы объяснить ряд происходящих явлений в рамках классической физики. Предположение о том, что при увеличении скорости увеличивается масса электрона, высказал в 1881 году Джозеф Томсон. В опытах по отклонению электронов, движущихся с различными скоростями, в постоянном магнитном поле, он обнаружил, что быстрые электроны движутся не так, как это следовало из законов Ньютона и предположения о постоянстве массы. Из двух постулатов классической физики, предположения о постоянстве массы и предположения о верности формулы 
Джозеф Томсон решил отказаться от предположения о постоянстве массы тела при больших скоростях. Это предположение развили Макс Абрагам и Гендрик Лоренц в рамках теории эфира Лоренца. Абрагам, для описания экспериментально полученной зависимости массы электрона от его скорости, предложил эмпирическую формулу 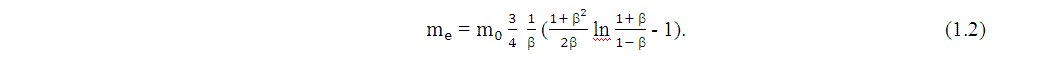
В этой формуле m0 - масса покоя электрона, me - масса движущегося электрона, а величина β = v/c - отношение скорости электрона к скорости света. Лоренц предложил другую формулу, которую он вывел исходя из предположения, что формулы электродинамики Максвелла верны и для движущихся относительно эфира систем отсчета, и для неподвижных относительно эфира систем отсчета. Предложенная Лоренцем формула выглядела так: 
Абрагам и Лоренц, как и Томсон, исходили из предположения, что формула Ньютона верна и движущийся с большой скоростью электрон в магнитном поле ускоряется значительно меньше потому, что его масса возросла. Альберт Эйнштейн тоже пишет об этом явлении, как об увеличении релятивистской массы тела с ростом скорости. Чаще всего он пропускает слово "релятивистской" и пишет просто об увеличении массы тела. И он рассматривает увеличение массы любого тела, которое движется со скоростями, близкими к скорости света, а не только увеличение массы электрически заряженного электрона. Так, в статье 1907 года "О принципах относительности и его следствиях", он высказывает предположение, что при увеличении относительной скорости объекта возрастает не только инертная, но гравитационная масса тела. В то же время, есть принципиальная разница в подходах к этому явлению. Томсон рассматривал увеличение массы электрона как абсолютное явление, то есть, увеличение массы, которое не зависит от того, в какой системе отсчета производится измерение. Если бы мы жили в физическом мире по Томсону, то физики, оказавшиеся в замкнутом пространстве, могли бы определить свою абсолютную скорость, просто точно измерив массу своего тела. В теории эфира Лоренца, физики в замкнутом пространстве уже не смогли бы определить свою скорость относительно неподвижной системы отсчета, измерив массу своего тела. В этой теории, масса тела, с ростом его скорости относительно физического эфира увеличивается, но, вместе с увеличением массы тела, изменяются его размеры и ход времени, а поэтому возникает "физическая иллюзия ([4] стр. 220)" того, что ничего не изменилось. Как это ни странно, именно так очень часто трактуют и теорию относительности. Примечание: Определение "физическая иллюзия", для описания теории эфира Лоренца, взято из книги Макса Борна "Эйнштейновская теория относительности", [4] стр. 220. Уже в ранних работах по теории относительности, Эйнштейн высказывает предположение, что масса тела напрямую зависит от его энергии: "всякая инертная масса представляет собой запас энергии".([1] стр. 94) Согласно этому предположению, любое тело само по себе обладает значительной энергией, и поэтому, когда оно покоится в некоторой системе отсчета, в этой системе отсчета оно обладает определенной массой, массой покоя. А любое тело, которое движется, относительно выбранной системы отсчета, кроме энергии покоя и связанной с ней массой, обладает еще кинетической энергией и поэтому, от добавочной энергии, его масса увеличивается. В такой трактовке, масса тела зависит от относительной скорости движения объекта, но в системе отсчета связанной с самим объектом, его масса всегда остается постоянной. И это уже не "физическая иллюзия", а реальный факт. И в такой физической системе мира, физики в замкнутом помещении тоже не смогут измерить свою скорость, измеряя свою массу, потому что относительно самих себя они неподвижны, с какой бы скоростью ни двигались относительно Земли. Вероятно, до конца своей жизни Эйнштейн был убежден в том, что с ростом скорости масса тела возрастает. Исключением, пожалуй, была статья 1935 года "Элементарный вывод эквивалентности массы и энергии". В этой статье, ссылаясь на работу профессора Биркхофа "Relativity and Modern Physics" ("Относительность и современная физика"), Эйнштейн приводит доводы в пользу того, что правильнее считать массу тела постоянной величиной. Поясню, о чем идет речь. В классической физике инертная масса тела определяется по уравнению движения: 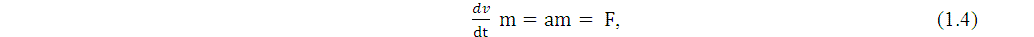
где: v - скорость тела, t - время, m - инертная масса, a - ускорение, F - сила, действующая на тело. В этой формуле на некоторое тело воздействует сила F и оно за малый промежуток времени dt изменяет свою скорость в пространстве на величину dv. А масса тела m в данном случае показывает способность тела "сопротивляться" воздействию внешней силы. Масса тела в таком эксперименте выступает как мера инертности тела и часто называется инертной массой тела. В теории относительности в этой формуле появился еще один коэффициент γ : 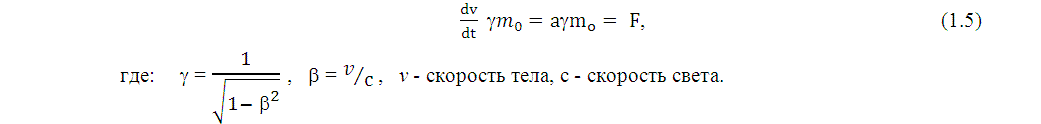
Здесь на тело тоже воздействует сила F и тело изменяет, под действием этой силы, свою скорость. И нужно определить к чему относится коэффициент γ, к ускорению тела или к мере инертности тела. То есть, весь вопрос сводился к тому, что считать настоящей массой тела, массу покоя m0 или релятивистскую массу mр = γ m0. В. А. Угаров в книге "Специальная теория относительности", пишет по этому вопросу: "Следует ли вводить релятивистскую массу - вопрос чисто методический. Если считать массу mр просто сокращенным обозначением, то вопроса вообще не возникает. Но совсем другое дело - физическая интерпретация релятивистской механики. Здесь нередко возникают недоразумения и туманные истолкования". ([5 стр. 338]) Позволю себе конкретно по этому вопросу не согласиться с В. А. Угаровым. Недоразумения и туманные истолкования пошли с легкой руки Альберта Эйнштейна, который как раз и считал релятивистскую массу мерой инертности физического тела. И эти "недоразумения и неясные толкования" вошли в классические труды Макса Борна ([4 стр. 272]) и во многие современные учебники физики. Понятно, что Эйнштейн стремился сохранить изначальный смысл формулы Ньютона F = dv/dt m, и классическое определение инертности тела. Вот только с предложенным Эйнштейном определением массы возникают сложности. Пока мы рассматриваем законы сохранения для движения объектов вдоль одной прямой, все в порядке, и оба определения массы, и m0, и mр = γ m0, совершенно равноправны. Сложности возникают, когда мы начинаем рассматривать законы сохранения на плоскости или в трех измерениях. В статье 1935 года "Элементарный вывод эквивалентности массы и энергии" Эйнштейн упоминает об исследованиях по наблюдению столкновений элементарных частиц. Конкретно, он ссылается на исследования неупругих столкновений элементарных частиц. Можно упомянуть по этому поводу также эксперименты по упругому рассеянию частиц, которые проводились в Дубне, в результате которых физики пришли к аналогичным выводам. И одни, и другие эксперименты будут подробнее рассмотрены в следующих главах, но вкратце, их суть в том, что изучались углы разлета элементарных частиц при столкновениях, в зависимости от их скорости и массы. Для того, чтобы объяснить наблюдаемые углы разлета элементарных частиц при столкновениях, при условии, что массой считается релятивистская масса mр = γ m0 , оказалось необходимым ввести представления о двух инертных массах тела, продольной и поперечной. В связи с этим, в теории относительности появилось понятие "тензор масс": 
В этой диагональной матрице, единица в верхнем левом углу связана с массой тела в направлении его движения (например, вдоль оси x), а два коэффициента γ-2 дают поправки к массе тела для перпендикулярных движению направлений (осей y и z). Если же считать массой тела его массу покоя, таких проблем не возникает, и масса тела одинакова во всех направлениях. Угаров приводит еще целый ряд преимуществ использования массы покоя в качестве "настоящей" массы тела ([5 стр. 338]), но всё это технические преимущества, преимущества связанные с удобством вычислений. Но вопрос о том, что в действительности является массой тела, носит концептуальный характер и здесь, прежде всего, нужно исходить из безусловного приоритета первого принципа относительности Эйнштейна. А при таком подходе, мы должны принять, что настоящей величиной массы тела является та величина массы, которая измеряется в собственной системе отсчета, то есть, при таком подходе, мы должны признать, что масса покоя и есть "настоящая" масса тела. Здесь может возникнуть естественный вопрос о том, как в таком случае быть с определением массы тела, как меры его инертности, то есть, способности сопротивляться приложенной к ней силе. Эйнштейн следовал наиболее естественному выбору: есть сила F, действующая на тело, есть ускорение a = dv/dt , и есть релятивистская масса mр, которая определяет то, как связаны между собой сила и ускорение: 
Если мы отказываемся от релятивистской массы, как от меры инертности тела, и в качестве оной признаем "массу покоя", то коэффициент γ придется перенести в другую часть уравнения: 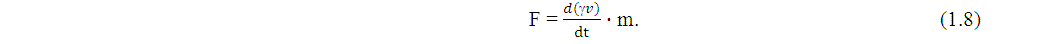
Таким образом, оказывается, что мы должны мерой инертности тела m связать между собой силу F и некую непонятную величину γv. Это непривычно, но, на мой взгляд, это одно из самых перспективных направлений в дальнейшем развитии теории относительности. Приведенная выше формула, это уже полшага к принятию концепции пространства релятивистских скоростей, скоростей, которые исчисляются по правилам геометрии Лобачевского, и которые должны применяться вместо скоростей классической физики в основных законах кинематики, и принципиально новому философскому переосмыслению теории относительности. Таким образом, на начало двадцать первого века в физике сосуществуют, по крайней мере, несколько трактовок теории относительности, в некоторых из них массой тела принято считать релятивистскую массу, и считается, что величина массы зависит от скорости. В других трактовках, "настоящей" массой тела принято считать масса покоя, и величина массы считается инвариантом, то есть величиной постоянной в любой инерциальной системе отсчета. Если вас интересует эта тема, рекомендую к прочтению статью Л. Б Окуня "Понятие массы" [6], которая была опубликована в июльском номере журнала "Успехи физических наук" за 1989 год. Статья доступна на официальном сайте журнала http://ufn.ru/. В своей очень подробной статье по этому вопросу, Окунь отмечает, что представления о том, что масса тела меняется в зависимости от его скорости, приводятся в основном в популярной литературе, школьных и вузовских учебниках. В серьезных монографиях по теории относительности уже давно признано, что масса покоя тела это и есть его настоящая масса, и эта величина инвариант [6 стр. 512], то есть, не зависит от выбранной системы отсчета. С представлениями о том, что масса тела постоянная величина, произошла история, чем-то похожая на ту, которая произошла со вторым принципом теории относительности. Второй принцип заключается в том, что в любой инерциальной системе отсчета скорость света остается постоянной величиной. Это означает, что измеряя скорость распространения света в том помещении, где они оказались, физики, из нашего мысленного эксперимента с замкнутым пространством, не смогут определить, с какой скоростью они движутся относительно Земли. Но в истории развития теории относительности был период, примерно 1910-1914 года, когда Эйнштейна работал над ранними вариантами теории гравитации. В этих работах Эйнштейн отказывался от принципа постоянства скорости света для пространств с сильными гравитационными полями. Этот период закончился в 1915 году созданием общей теорией относительности, в которой принцип постоянства скорости света был восстановлен. И это событие имело свою цену, Эйнштейн был вынужден отказаться от своих ранних воззрений на свойства физического пространства. До 1915 года Эйнштейн решительно выступал против существования эфира и этому был посвящен целый ряд его публикаций. После 1915 года Эйнштейн приходит к концепции релятивистского эфира. Он по-прежнему выступает против классической трактовки физического эфира, но вместе с тем пишет, что без концепции эфира создать теорию поля невозможно. В популярной литературе по теории относительности этот факт тоже практически не отражен, хотя он очень важен для понимания этой теории. Впрочем, этот факт практически не отражен и в учебниках. Изложенная в учебниках версия общей теории относительности скорее похожа на трактовку, изложенную в книге Макса Борна "Эйнштейновская теория относительности", в которой вся информация о релятивистском эфире Эйнштейна отсутствует, а вместо него приводится концепция трехмерного поля. В своих ранних работах, Эйнштейн рассматривает физическое пространство как трехмерное нечто, абсолютно лишенное физических свойств, просто как вместилище для материальных объектов. Позже, к пространству присоединилось время, и речь пошла о пространственно-временном континууме, пока еще только в рамках геометрии Минковского. В общей теории относительности Эйнштейн приходит к выводу, что пространство может быть искривлено под действием гравитационного поля и под действием искривленного пространства-времени происходит притяжение физических объектов. Таким образом, само пространство стало рассматриваться как еще один физический объект, обладающий вполне определенными физическими свойствами. На свойства пространства можно воздействовать и свойства пространства воздействуют на другие объекты, и эти свойства можно измерить. На этой основе после 1915г. произошло сближение взглядов Лоренца и Эйнштейна. Это был компромисс, при котором Лоренц отказался от своих ранних идей абсолютного пространства, а Эйнштейн признал существование пространства как физического объекта и заговорил об эфире совсем иначе: "в общей теории относительности даже пустое пространство имеет физические свойства. Последние характеризуются математически компонентами гравитационного потенциала, которые определяют как гравитационное поле, так и метрические свойства этой области пространства. Это положение удобно понимать в том смысле, что речь идет о некотором эфире, состояние которого непрерывно изменяется от точки к точке. Нужно только остерегаться приписывать этому "эфиру" материальные свойства (например, определенную скорость в каждой точке)".([1; стр. 625]) "Наши сомнения относительно реальности волнового поля усиливаются еще и тем обстоятельством, что согласно теории Бора частота испускаемого излучения не определяется электрическими массами, совершающими периодические движения с той же частотой. Но даже если эта возможность созреет в подлинную теорию, мы не можем в теоретической физике обойтись без эфира, т. е. континуума, наделенного физическими свойствами, ибо общая теория относительности, основных идей которой физики, вероятно, будут придерживаться всегда, исключает непосредственное дальнодействие; каждая же теория близкодействия предполагает наличие непрерывных полей, а, следовательно, существование "эфира" [2; стр. 160]История отказа от представлений о постоянстве массы тела, заняла намного больше времени. Началась она в 1881 году с работ Джозефа Томсона, и еще не закончилась до сих пор, раз в учебниках приводится информация о зависимости массы от скорости. Но возврат к представлениям о постоянстве массы тела тоже имеет свою цену. И цена эта - пересмотр старых представлений о сущности физических скоростей. Отчасти ознакомиться с этим пересмотром можно по статье советского физика Н. А. Черникова "Геометрия Лобачевского и релятивистская механика", опубликованной в 1973 году в сборнике "Физика элементарных частиц и атомного ядра" Объединенного института ядерных исследований в городе Дубна. Представления о том, что масса тела зависит от его скорости, характерны для переходного периода от представлений классической физики к последовательному использованию принципов относительности Эйнштейна. И то, что этот процесс затянулся на десятилетия, лишь подчеркивает постепенность этого перехода, не только в популярной литературе по теории относительности, но и в теоретической физике. Но если в представлениях о природе массы тел, в физике произошли определенные изменения, то есть целый ряд вопросов, которых эти изменения не коснулись. Вот, к примеру, в книге Угарова приводится такая критика использования релятивистской массы: "Как и в классической механике, мы хотим связать массу со свойствами самой частицы, и тогда единственный разумный способ введения массы состоит в том, чтобы пользоваться массой покоя. Можно сказать, конечно, что ускорение частицы и достижение ею релятивистской скорости вызывают изменение ее внутренних свойств и, в частности, массы. Однако можно совсем не трогать частицу, а перейти в другую ИСО, а в результате уравнение движения этой частицы по-прежнему будет 
Таким образом, если непосредственно принимать за чистую монету "релятивистскую массу", то она растет без всяких физических причин. Едва ли такой результат можно считать удовлетворительным". Стоит прислушаться к этому мнению, но особенно интересна фраза "вызывают изменение ее внутренних свойств и, в частности, массы". У любого объекта кроме массы есть и другие свойства, например такие, как размеры и ход времени. И по отношению к этим свойствам объектов можно в той же мере потребовать безусловного приоритета принципа относительности, как и в отношении массы. Слишком часто в работах, посвященных теории относительности, даже в работах классиков, звучат утверждения о том, что у движущихся тел сокращаются размеры и замедляется ход времени. Но, при этом, чаще всего, ничего не говорится о том, что такие эффекты, это следствие применения методик измерения длин и промежутков времени, взятых из классической физики и применяемых в той области, для которой они не предназначены. 2. Определение релятивистского пространства скоростей
Термин "релятивистское пространство скоростей" используется в ряде источников по теории относительности, в частности, можно рекомендовать статьи Н. А. Черникова "Геометрия Лобачевского и релятивистская механика" [9] и "Трудные вопросы теории относительности" [10], а также, книгу В. Н. Дубровский, Я. А. Смородинский, Е. Л. Сурков "Релятивистский мир" [11]. Как и в случае "пространства скоростей" в классической физике, речь идет не о физическом пространстве, которое нас окружает, а скорее о пространстве математическом, векторном. Такие пространства часто используют физики теоретики для описания своих моделей. Тем не менее, эти пространства, как и в данном случае, описывают реальные свойства окружающего нас физического мира, и отображают его реальные свойства. Н. А. Черников дает такое определение пространства скоростей: "Постараемся составить самое элементарное представление о пространстве скоростей. Это такое пространство, в котором компоненты скорости v1, v2, v3 являются координатами ".[9] В пространстве скоростей положение разных точек показывают не расстояние объектов друг от друга, а только их относительные скорости: "Расстояние в пространстве скоростей измеряется в единицах скорости, а не длины, и называется быстротой. Уже поэтому пространство скоростей не совпадает с пространством положений частицы ".[9] В классической физике пространство скоростей, как и физическое пространство, считается евклидовым, и для решаемого классической физикой круга задач, такое предположение вполне оправдано. Примеры использования классического пространства скоростей для решения задач по упругому столкновению элементарных частиц, которые движутся с относительными скоростями значительно меньше скорости света, можно найти в статье Я. А. Смородинский Е. А. Сурков "Геометрия столкновений", журнал "Квант" ?5 1970г. В классическом пространстве скоростей законы сложения и вычитания относительных скоростей объектов соответствуют обычным законам сложения и вычитания векторов в евклидовом пространстве. Например, если два объекта A и B движутся в пространстве относительно объекта O со скоростями v и u, в разных направлениях, то эти скорости можно обозначить двумя векторами v = |OA| и u = |OB| (рис. 1). 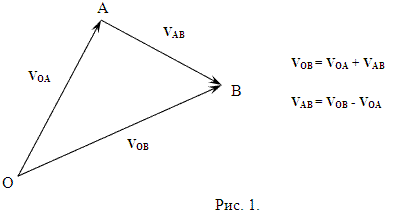
Положение точек O, A и B в классическом пространстве скоростей соответствуют относительным скоростям объектов O, A и B. Так, например, расстояние между точками O и A пропорционально скорости, с которой объект A движется относительно объекта A. То же самое касается и всех остальных пар точек. Прямая линия, проходящая через точки O и A, соответствует направлению, в котором изменяется расстояние между объектом O и объектом A. То же самое касается и всех остальных прямых. И когда все это происходит в классическом пространстве скоростей, то сумма углов в полученном треугольнике OAB всегда равна 180 . И, что самое главное, отображенный на евклидову плоскость треугольник пространства скоростей выглядит совершенно одинаково в любой системе отсчета, и с точки зрения наблюдателя из точки O, и с точки зрения движущихся относительно него наблюдателей A и B. 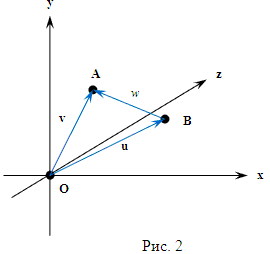
Когда же мы рассматриваем тела, движущиеся со скоростями сравнимыми со скоростью света, правила сложения скоростей в классическом евклидовом пространстве уже не работают. Например, в векторной форме (рис. 2) закон вычитания скоростей выглядит так: 
Где: v (vx,vy,vz) - вектор скорости объекта A, в системе отсчета O (x,y,z), u (ux,uy,uz) - вектор скорости объекта B, относительно системы отсчета O (x,y,z), с - скорость света, w - скалярная величина, равная скорости объекта A, относительно объекта B. В этой формуле vu = vu cos φ O - скалярное произведение вектора v на вектор u, которое равно произведению длин этих векторов на косинус угла между ними. Зная координаты векторов в ортонормированной системе координат , можно определить скалярное произведение по формуле: vu = vxux + vyuy + vzuz. Величина (v - u)2 тоже является скалярным произведением разности векторов v и u на себя: (v-u)2 = (vx - ux)2 + (vy - uy)2 + (vz - uz)2. Кроме того, в числителе этой формулы есть квадрат векторного произведения [vu]2. Векторным произведением векторов v и u является вектор q(qx,qy,qz), перпендикулярный векторам v и u, который для ортонормированного, положительно ориентированного базиса , можно определить по формуле: 
Где: x, y и z - единичные векторы, задающие базис. Таким образом, компоненты вектора q можно найти по формулам: 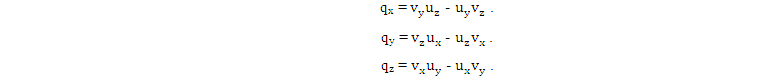
А скалярное произведение qq = q2 = [vu]2, соответственно, можно найти по формуле: 
Используя эти подсказки, вычислить значение w, по известным компонентам векторов скоростей, уже не трудно. Когда в пространстве скоростей точки O, A и B находятся на одной прямой, эти формулы сильно упрощаются, особенно, если эта прямая является координатной осью. Если векторы v и u коллинеарны (параллельны или направлены в противоположные стороны), то векторное произведение [vu] равно нулю и формула упрощается. В этом случае проводим ось координат через точки O, A и B и получаем схему на рисунке 3. Теперь, после упрощения формулы 2.1, разность скоростей для параллельных векторов можно найти по формуле: 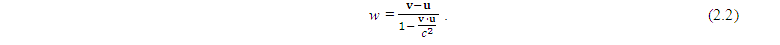
Если параллельные векторы v и u направлены в одну сторону (рис. 3), то найденная по этой формуле разность скоростей w, объектов A и B, окажется больше обычной арифметической разности скоростей v и u. 
По учебникам физики и популярным изданиям по теории относительности, больше известна формула сложения скоростей: 
В этой формуле: v - скорость объекта A в системе отсчета O, u - скорость объекта B, относительно объекта A, w - скорость объекта B в системе отсчета O, она же, сумма скоростей v и u. 
В этом случае, если векторы скоростей v и u направлены в одну сторону (рис. 4), относительная скорость w объекта B относительно системы отсчета O оказывается меньше, чем арифметическая сумма скоростей v и u. Соответственно, в векторной форме закон сложения скоростей в трехмерном евклидовом пространстве будет выглядеть так: 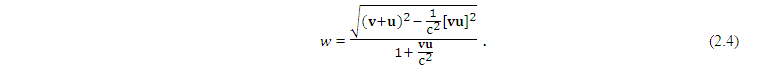
Следует отметить, что эти формулы предназначены для использования в классическом евклидовом пространстве скоростей, в котором скорость объекта определена просто как отношение пути, проходимого объектом в евклидовом пространстве за единицу времени, с точки зрения наблюдателя, который считает себя неподвижным, или относительно некоторого объекта, принятого за начало отсчета. Казалось бы, чего еще желать? Есть классическое определение скорости, которое себя зарекомендовало за тысячи лет практического использования. И есть скорости, близкие к скорости света, для которых законы сложения и вычитания скоростей сложнее, чем в классической физике. Зачем Н. А. Черников и другие исследователи вводят понятие "релятивистского пространства скоростей", и чем отличается скорости в такой трактовке от скоростей классических? Обратим внимание на то, что результат формулы 2.1, так же, как и формулы 2.4, величина w, является не вектором, а скаляром, то есть, не показывает направления скорости объекта A относительно объекта B, а просто равен относительной скорости между ними. В этом есть определенный смысл. Мы находим абсолютную величину вектора, но его направление в евклидовом пространстве неопределенно. Схема, приведенная на рисунке 2, на самом деле, будет верна только в том случае, когда скорость объектов A и B, относительно объекта O, значительно меньше скорости света. В случае больших скоростей, на ней искаженно изображены длина вектора |BA| и искаженно изображены величины углов В случае, когда относительные скорости объектов сравнимы со скоростью света, в эту схему нужно внести некоторые изменения. Например, такие изменения, как на рисунке 5. 
Теперь схема тоже представлена с искажениями, например, искажена реальная величина вектора |BA|. Но в этой интерпретации, правильно отображаются координаты скоростей A и B, относительно объекта O в ортогональном базисе (x,y,z), правильно отображаются величины отрезков |OA| и |OB|, правильно отображаются координаты отдельных точек отрезка |ВA| и правильно отображаются величины всех углов треугольника OAB. Отметим, что вообще без искажений, нарисовать эту схему на евклидовой плоскости невозможно. Если ту же самую схему рассматривать в системе координат объекта A, то оно будет выглядеть вот так (рис. 6): 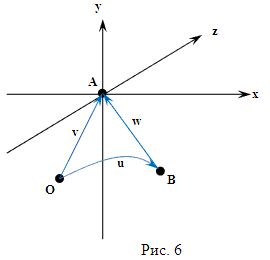
Величины углов треугольника OAB при изменении системы отсчета остались такими же, как и на схеме на рисунке 5. И теперь, без искажений отображается величина отрезка |BA|. В системе отсчета объекта B, эта же самая схема будет выглядеть так, как изображено на рисунке 7. На всех трех схемах треугольник OAB изображен по-разному. Но во всех трех случаях сумма углов треугольника оказывается равным одной величине и эта величина меньше чем 180 . Кроме этого, если рассмотреть любой вектор в разных системах отсчета, например вектор w на рисунке 6 и на рисунке 7, то окажется, что он направлен в разных направлениях. 
На евклидовой плоскости и в евклидовом трехмерном пространстве такое невозможно, но есть геометрия, в которой это нормальное явление. И эта геометрия, которая была открыта в первой половине 19 века и была впервые опубликована российским математиком Лобачевским. Небольшой участок плоскости Лобачевского можно достаточно точно отобразить в евклидовом пространстве в виде "седловины" (рис. 8). Целиком изобразить плоскость Лобачевского в трехмерном евклидовом пространстве без значительных искажений невозможно. 
Именно на поверхности этой фигуры, как и в любом месте плоскости Лобачевского, сумма углов треугольника оказывается меньше 180 и представленные на рисунках 4, 5 и 6 схемы будут отображены без искажений углов и сторон треугольников. Таким образом, получается, что скорости складываются и вычитаются не в привычном евклидовом пространстве, а в пространстве Лобачевского. Связь между теорией относительности и геометрией Лобачевского была обнаружена уже через несколько лет, после появления первой статьи Эйнштейна о принципах относительности, но в большинстве источников по теории относительности эта связь не показана в достаточной мере. В статье "Геометрия Лобачевского и релятивистская механика" Н. А. Черников пишет: "За релятивистскую механику в физической аудитории агитировать не приходится: она является рабочим инструментом в физике высоких энергий. Но, применяя этот инструмент, не всегда знают, что имеют в основном дело с геометрией Лобачевского. А между тем - имеют, поскольку пространство скоростей в релятивистской механике является пространством Лобачевского. Незнание этого часто приводит к непроизводительной трате сил и, разумеется, затрудняет понимание самой релятивистской механики ". Говоря о "новой теории относительности" Черников имеет в виду теорию относительности Эйнштейна, в которой развивались "старые" принципы относительности Галилея. Связь между геометрией Лобачевского и свойствами пространственно-временного континуума была известна ведущим физикам еще во время создания общей теории относительности. Дело только в том, каким образом интерпретировалась эта связь и насколько явно признавалась в работах ведущих релятивистов. Далее в своей статье Черников пишет: "Существенно, что в новой теории относительности в пространство инерциальных систем вместо геометрии Евклида вводится геометрия Лобачевского. Не беремся судить, почему Эйнштейн не высказывался в печати по этому вопросу. Что же касается Пуанкаре, то он не осветил этот вопрос в своих печатных трудах, возможно, потому, что, подобно Гауссу, не желал слышать "крика беотийцев". Могу предположить, что я догадываюсь о причине таких опасений. Дело ведь не только в том чтобы связь между геометрией Лобачевского и теорией относительности выявить, необходимо еще и объяснить ее. Да еще быть не только услышанным, но и понятым другими физиками. И, возникает ощущение, что математически вычислив связи между геометрией Лобачевского и теорией относительности, отцы этой теории еще не в достаточной мере понимали глубинные причины этой связи. Они просто принимали эту связь как факт, но в своих трудах не объясняли ее причин. По крайней мере, никто из известных мне авторов, в том числе и авторов указанных в начале данного труда, не привели ясного и образного объяснения этой связи. Но это все лирическое отступление. А сейчас вернемся к концепции релятивистского пространства скоростей в интерпретации Н. А. Черникова. А предложение это состоит в следующем: "Так как термины "релятивистский" и "нерелятивистский" приходится считать чисто условными, то надо договориться, какой придавать им точный смысл. Пусть первый означает, что в пространстве скоростей действует геометрия Лобачевского, а второй - геометрия Евклида. В таком понимании общая часть нерелятивистской теории основывается на абсолютной геометрии пространства скоростей ". Согласно предложенной Н. А. Черенковым терминологии, очевидно, следует и "быстроту" называть релятивистской скоростью, но данный термин уже используется в другом значении, как классическая скорость, сравнимая по величине со скоростью света. Очевидно именно по этой причине, в книге "Релятивистский мир" авторы В. Н. Дубровский, Я. А. Смородинский и Е. Л. Сурков для обозначения скоростей, измеренных по правилам геометрии Лобачевского, используют нейтральный термин "V-скорости". Уильям Бёрке в книге "Пространство-время, геометрия, космология" эту же самую физическую величину, как и Черников, называет быстротой. Во всех этих источниках "V-скорости" и "быстрота" показаны просто как удобный математический, или, точнее, геометрический прием, который позволяет решать некоторые задачи по теории относительности. В данной работе я хочу показать, что значение этой физической величины очень сильно недооценено в современной физике. Более того, ее значение равно, или даже выше, чем значение обычной классической скорости. Используемый Бёрке термин "быстрота" не отражает в полной мере ни физического смысла этой величины, ни ее значения, это именно скорость, а не что-то другое. Термин "V-скорость" подразумевает, что это искусственная величина удобная в расчетах. Термин "релятивистская скорость" имеет смысл, по аналогии с термином "релятивистская масса", но, как уже было сказано, он используется в другом значении, и такое применение этого термина создаст путаницу. Все эти термины представляются неудачными, поскольку эта физическая величина напрямую связана не только с законом сложения скоростей, но и со вторым законом Ньютона, что будет показано в следующих главах. 3. Базовые принципы геометрии Минковского
Герман Минковский разработал теорию геометрии, описывающей пространственно-временной континуум и соответствующий преобразованиям Лоренца, в 1907 году, а опубликована его работа была уже после смерти, в 1909 году. И это открытие Германа Минковского, сразу перевело теорию относительности на принципиально новый уровень. И теперь можно было уверенно сказать, если Вы не понимаете геометрию Минковского, то не понимаете и теорию относительности в целом. По сути, можно заменить второй постулат относительности, то есть, постулат о постоянстве скорости света для любой системы отсчета, утверждением: метрика пространственно-временного континуума описывается геометрией Минковского. Это утверждение уже содержит в себе информацию о существовании максимально возможной скорости перемещения в пространстве и еще, дополнительно, описывает законы сложения скоростей, и многое другое, жизненно необходимое в теории относительности. По сложившейся традиции, максимальную скорость перемещения в пространстве принято называть скоростью света, хотя известно, что в воде или воздухе скорость распространения света значительно ниже максимально возможной скорости. С этим фактом, например, связан эффект Вавилова - Черенкова, то есть, свечение, возникающее в жидкости, при движении через нее частиц со скоростью большей, чем скорость света в этой жидкости. Точнее будет сформулировать так: в вакууме скорость распространения электромагнитного излучения (света) стремится к максимально возможной скорости, а поэтому мы с большой точностью можем считать, что максимально возможная скорость и скорость света в вакууме, это одно и то же. В теории относительности принято называть геометрию Минковского псевдоевклидовой. Такое определение создает путаницу, и многие люди считают геометрию Минковского очень похожей на евклидову. Это заблуждение. Геометрия Минковского это неевклидова геометрия, и она отличается от евклидовой геометрии значительно сильнее, чем, например, неевклидова геометрия Римана или неевклидова геометрия Лобачевского. В геометрии Минковского можно построить декартову прямоугольную систему координат, подобно тому, как это делается в евклидовой геометрии. Затем, можно отобразить объекты из геометрии Минковского на евклидову поверхность или в евклидовом пространстве так, чтобы координаты отобразились без искажений. Это, наверное, и является основным источником иллюзии того, что эти две геометрии похожи. Но на самом деле, когда мы отображаем объект из геометрии Минковского на евклидову плоскость, скажем, пытаемся нарисовать его на этом листе бумаги, то он, как правило, оказывается сильно искаженным. Объект геометрии Минковского, это обычно какой-то физический процесс, происходящий в пространстве и времени, а точки пространства Минковского, это некоторые события, происходящие в пространстве и времени. Значит, отображение событий и процессов из пространства Минковского на евклидову плоскость, на диаграмму Минковского, как правило, происходит с большими искажениями. Декартовы координаты можно перенести без искажений, а вот продолжительность физических процессов, если они не параллельны координатной оси времени, отображаются всегда с искажениями. С искажениями отображаются и расстояния (интервалы) между отдельными точками-событиями, если прямая между ними не параллельна оси координат. С искажениями отображаются углы между линиями в пространстве Минковского. Например, все векторы, исходящие из точки A, которые изображены на рисунке 9, имеют одинаковую длину в пространстве Минковского, но после отображения их на евклидову плоскость, возникает впечатление, что их длина различна. 
Проверить это утверждение можно, просто поворачивая в пространстве Минковского любой из этих векторов вокруг точки A: 
где: xk - координаты вектора до поворота, xi - координаты вектора после поворота, Tik - матрица ротационного преобразования. При таком повороте, вектор xk может совпасть с любым другим вектором xk, изображенным на рисунке, а конец вектора опишет на отображении в евклидовом пространстве гиперболу, показанную на рисунке 9. На самом деле, в пространстве Минковского, описанная концом вектора линия это аналог окружности в евклидовом пространстве, то есть, множество точек, которые расположены на одинаковом расстоянии от центра, то есть, от точки A. Кроме того, в пространстве Минковского существуют три вида линий, действительные (времяподобные), мнимые (пространственноподобные) и световые, но когда мы отображаем их на диаграмму Минковского, то все они отображаются на действительные линии евклидового пространства. Это тоже создает некоторую путаницу, поскольку очень многим людям не вполне ясна разница между этими тремя видами линий. Начнем с самого простого, с расстояний между точками-событиями в пространстве Минковского. В евклидовом трехмерном пространстве, пользуясь прямоугольной декартовой системой координат и зная координаты ((xa,ya,za) и (xb,yb,zb)) концов отрезка AB можно найти его длину по формуле 
В пространстве Минковского интервал, аналог расстояния, между двумя точками-событиями может быть найден по формуле 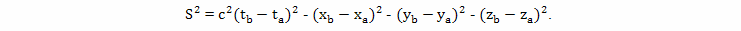
где: ta, xa, ya, za и t_b, xb, yb, zb - координаты точек-событий A и B, c - скорость света в вакууме. Или, можно определить временной интервал 
Если T2 - положительное число, то временной интервал T равен собственному времени, которое потребуется объекту на перемещение из события A в событие B, двигаясь равномерно и прямолинейно, без ускорений. Если T2 - отрицательное число, то его абсолютная величина будет равна времени, за которое, с точки зрения наблюдателя в системе отсчета, в которой события A и B произошли одновременно, свет пройдет расстояние между точками, в которых произошли эти события. Рассмотрим еще одно важное отличие между геометрией Минковского и евклидовой геометрией. Первый постулат геометрии Евклида звучит так: От всякой точки до всякой точки можно провести прямую линию. В геометрии Евклида есть точное описание прямой, которую можно провести от всякой точки до всякой точки. Эта прямая является упорядоченным, непрерывным и связанным множеством точек. Остальные свойства рассмотрим позже. Непрерывность и связанность точек прямой линии означает, что по этой линии можно двигаться, последовательно перемещаясь от одной точки к другой, без скачков и не покидая эту линию. Назовем прямую линию, обладающую такими свойствами, действительной прямой. В геометрии Минковского нельзя соединить действительной прямой линией любые два события, а значит, первый постулат евклидовой геометрии неверен. В геометрии Минковского можно сформулировать аналогичный постулат иначе: Некоторые пары точек можно соединить действительной прямой линией. Если в пространстве Минковского задана некоторая точка A, то точки (B1 и B2), которые можно соединить с точкой A действительной прямой линией, будут располагаться внутри конусообразной фигуры, показанной на рисунке 10. 
В качестве примера, показаны две точки B1 и B2, соединенные с событием A действительной прямой линией. Как видно из рисунка, точки, которые можно соединить с точкой A действительной прямой линией, образуют два отдельных множества, которые разделены точкой-событием A. Эти множества обозначены Ta+ и Ta-. Физическая интерпретация этих множеств такова. Множество Ta+ это абсолютное будущее, по отношению к событию A. Множество Ta- это абсолютное прошлое, по отношению событию A. Вместе эти два множества точек-событий могут быть определены как временные области. События, входящие в множества Ta+ и Ta-, могут быть непосредственно связаны с событием A причинно-следственными связями. То есть, любое из событий входящих в множество Ta- могут повлиять на происходящее в событии A, то есть, быть причиной, по отношению к событию A. В свою очередь, событие A может повлиять на события входящие в множество Ta+, так, что эти события станут следствием по отношению к событию A. Определить, принадлежит ли некоторое событие B к множеству Ta+ или Ta-, можно зная координаты этого события. Если выполняются условия: 
тогда, событие B принадлежит множеству Ta+. Если выполняются условия: 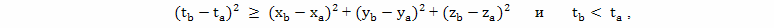
тогда, событие B принадлежит множеству Ta-. Иначе, событие B не принадлежит ни к области абсолютного будущего, ни к области абсолютного прошлого. И тогда, провести прямую действительную линию между точками A и B невозможно. Границей множеств Ta+ и Ta- являются конусообразные множества точек-событий Ca+ и Ca-, которые принято называть световыми конусами. В событие A можно попасть из любой точки множества Ca-, только в том случае, если двигаться по прямой линии и со скоростью света в вакууме. Для того чтобы разогнать до такой скорости, любое тело или любую частицу, имеющую ненулевую массу, им необходимо сообщить бесконечно большую энергию, а значит, это практически невозможно. То есть, двигаться с такой скоростью может только частица, не имеющая массы. Такой частицей, например, может быть квант света, масса которого считается равной нулю. Физическая интерпретация множества событий Ca+ аналогична. Это те события, в которые можно попасть, двигаясь из события A по прямой линии и со скоростью света в вакууме. Образующие световой конус прямые называют световыми прямыми. Событие B принадлежит к световому конусу Ca+, если ее координаты удовлетворяют условиям: 
И событие B принадлежит к световому конусу Ca-, если ее координаты удовлетворяют условиям: 
Множество точек-событий, которые не принадлежат ни множеству Ta+, ни множеству Ta-, ни к световым конусам Ca+ и Ca-, образуют еще одно множество Sa- пространственную область, относительно точки A. Ни одна из точек, попадающих в область Sa, не может быть соединена с точкой A действительной прямой линией. События, попадающие в область Sa, не могут быть непосредственно связаны с событием A причинно-следственными связями. То есть, никакое из событий, входящих в множество Sa не могут быть ни причиной, ни следствием, по отношению к событию A. В пространственную область попадают точки, координаты которых удовлетворяют следующему условию: 
Используя определения множеств в координатах, можно доказать следующее. Если точка-событие B находится в пространственной области, по отношению к точке A, то верно и обратное, то есть, точка A находится в пространственной области, относительно точки B. Если B ∈ Sa, то: A ∈ Sb. Аналогично, можно доказать следующие соотношения: Если B ∈ Ta+, то: A ∈ Tb-. Если B ∈ Ta-, то: A ∈ Tb+. Если B ∈ Ca+, то: A ∈ Cb-. Если B ∈ Ca-, то: A ∈ Cb+ . Таким образом, свойство нахождения точек-событий во временной области, пространственной области или на световом конусе, взаимно. Также, можно доказать следующее. Если две точки A и B находятся в пространственной области, по отношению друг к другу, то всегда существует такая точка D, которая расположена в области абсолютного будущего или в области абсолютного прошлого, по отношению к точкам A и B. То есть, символически это можно выразить так: Если B ∈ Sa, то, всегда существует такая точка D, что: D ∈ Ta+ и D ∈ Tb+. А также: Если B ∈ Sa, то, всегда существует такая точка D, что: D ∈ Ta- и D ∈ Tb-. И это означает, что в геометрии Минковского действует следующее правило: Любую пару точек в пространстве Минковского, расположенную пространственной области относительно друг друга, можно соединить ломаной линией, состоящей из двух отрезков действительных прямых линий. Например, так, как это показано на рисунке 11. 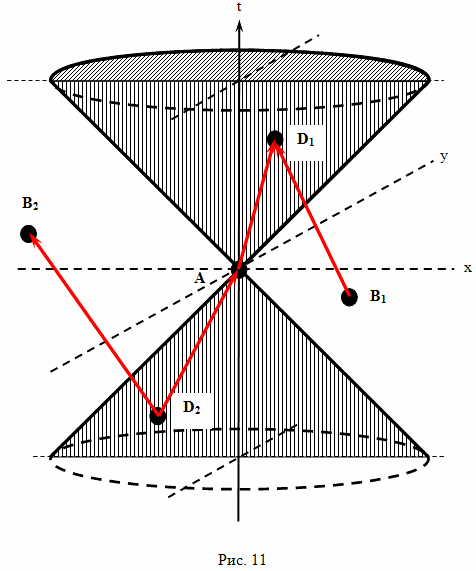
Временной интервал между двумя точками, находящимися относительно друг друга в пространственной области, равен мнимому числу. Если: 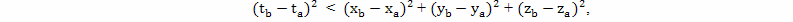
то величина выражения 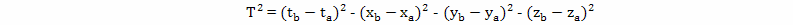
меньше нуля, а такое может быть, только если T мнимое число. Можно показать, что две точки A и B, расположенные в пространственной области, по отношению друг к другу, могут быть сколь угодно близки, можно сказать, бесконечно близки. И тогда, величина временного интервала между ними стремится к бесконечно малому мнимому числу. Последовательно собрав множество таких точек, точка за точкой, можно построить мнимую линию. От действительной линии она будет отличаться тем, что движение вдоль этой линии невозможно. На множестве точек, которые принадлежат мнимой прямой, эти точки никак не связаны между собой. То есть, если вырезать такую мнимую прямую из содержащего его пространства, ее точки не останутся связанными между собой и распадутся на бесконечное множество отдельных точек. И, не зная, как эти точки связаны друг с другом через окружающее их пространство, даже определить, в какой последовательности их нужно располагать, невозможно. В геометрии Минковского, описывающей пространственно-временной континуум и содержащей три пространственных измерения, подобным образом можно построить не только мнимые линии, но и двухмерные мнимые поверхности, и трехмерные мнимые пространства. Например, можно построить трехмерную мнимую евклидову гиперплоскость. От трехмерного евклидового пространства такая мнимая гиперплоскость будет отличаться тем, что отдельные точки-события в ней не будут непосредственно связанны между собой и движение по ней будет невозможно.На физической интерпретации изложенной выше концепции, стоит остановиться подробнее. В последние два десятилетия девятнадцатого века ученые физики сделали ряд значительных открытий. В 1881 году Джозеф Томсон, экспериментируя с прадедушкой телевизионного кинескопа, изучал отклонение луча электронов в постоянном магнитном поле. И он обнаружил явление, которое он счел увеличением массы электронов при росте их скорости. По данным его исследований, при определенной скорости, которую позже стали обозначать символом c, дальнейшее увеличение скорости становилось невозможным. Потом обнаружилось, что это ограничение скорости действует и при распространении электромагнитных волн, поэтому это явление приписали всем заряженным частицам. Следующим шагом стало обнаружение, что световые волны распространяются с той же скоростью, что и электромагнитное излучение, и было высказано предположение, что видимый свет это высокочастотное электромагнитное излучение. А еще через некоторое время, в теории эфира Лоренца, ограничение скорости величиной c предполагается свойством всех без исключения тел, а не только электрически заряженных частиц. Это предыстория создания теории относительности, но до сих пор, в источниках по теории относительности можно встретить объяснения, которые заключаются в том, что свойства обычного вещества и электромагнитного излучения таковы, что оно не может двигаться в пространстве быстрее скорости света. И так возникают гипотезы о существовании особого вещества, особых частиц, тахионов, которые двигаются только со скоростью больше скорости света. Однако если допустить существование тахионов, то легко показать, что либо неверны базовые принципы теории относительности, либо возможна машина времени, двигающаяся в прошлое. Возможность существования тахионов тоже выводится из формул теории относительности, только возможность, и то, при условии, что мнимые линии трактуются как направления, в которых могут двигаться только тахионы. Но на самом деле, исходным постулатом геометрии Минковского была невозможность причинно-следственных связей между событиями, расположенными, друг относительно друга, в пространственной области. И, из базовых принципов геометрии Минковского следует, что движение со скоростью больше световой невозможно вовсе не потому, что свойства обычного вещества не позволяют ему двигаться в пространстве быстрее определенной скорости, такое предположение приводит к чему-то очень похожему на теорию эфира Лоренца. Согласно геометрии Минковского, если представить себе мировую линию объекта, движущегося быстрее скорости света, то отдельные точки-события этой линии окажутся несвязанными между собой причинно-следственными связями. И, хотя такую линию можно нарисовать на схеме в евклидовом пространстве (рис. 12), в реальном пространственно-временном континууме просто нет такого направления. И дело не в свойствах частиц, а в свойствах самого пространства. 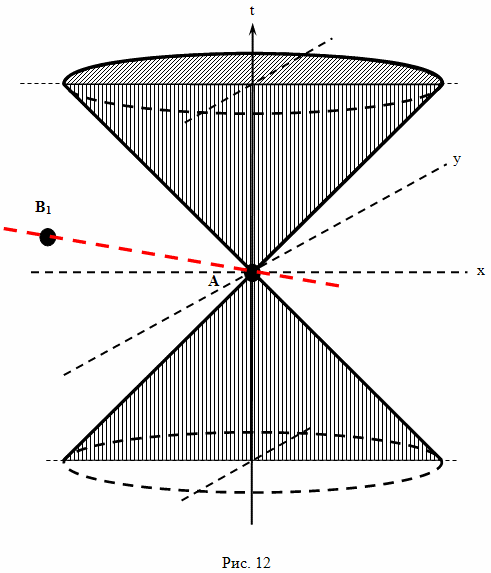
И еще один нюанс. Раз в любой, произвольно взятой пространственной трехмерной гиперплоскости события не могут быть связаны между собой причинно-следственными связями, раз никакое взаимодействие и никакой сигнал не может связать между собой события, расположенные в любой пространственной гиперплоскости, то только процессы, происходящие во времени, связывают пространство нашего мира в единое целое. 4. Тригонометрия в пространстве Минковского
Многие задачи теории относительности значительно легче и нагляднее решаются при помощи геометрических методов. При таком подходе, длина любой действительной линии в пространстве Минковского, мировой линии в пространственно-временном континууме, пропорциональна интервалу собственного времени объекта, который двигался по этой линии. Это утверждение верно для объектов движущихся инерциально, в таком случае, мировая линия будет выглядеть на диаграмме Минковского как прямая линия между двумя событиями, например A и B. А интервал собственного времени, объекта, который двигался прямолинейно и неускоренно из события A в событие B, будет равен временному интервалу между этими событиями в пространстве Минковского. Это утверждение верно и для объектов, которые двигались ускоренно. Но в этом случае, мировая линия объекта будет искривлена, длина этой линии в пространстве Минковского будет равна времени прошедшему между событиями A и B по собственным часам движущегося объекта. И конечно, собственное время, измеренное по кривой, будет отличаться от интервала времени измеренному по прямой линии между событиями A и B в пространстве Минковского. И здесь есть еще одно существенное отличие геометрии Минковского от геометрии Евклида. В евклидовой геометрии прямая линия это всегда кратчайшее расстояние между двумя точками. В геометрии Минковского такое утверждение неверно. Действительная прямая линия между событиями A и B не является кратчайшим путем между этими событиями, но она не является и самым длинным путем среди всех возможных путей. Чтобы определить прямую линию через расстояние между точками, введем понятие последовательный путь. Последовательный путь из события A в событие B, это такой путь, в пространстве Минковского, при котором расстояние от события A до движущейся по пути точки C монотонно растет, а расстояние от движущейся точки C до события B монотонно уменьшается. Физически, если Вы движетесь из события A в событие B из прошлого в будущее, не меняя направления хода времени, это и будет последовательный путь. Теперь можно дать определение прямой линии. В пространстве Минковского прямая линия между событиями A и B, это самый длинный путь на множестве последовательных путей из события A в событие B. Назовем это явление инверсией свойств прямой линии. Рассмотрим это на нескольких примерах. Простейший пример это свойства действительного треугольника, то есть, треугольника, все стороны которого отрезки действительных прямых линий, а вершины - некоторые события в пространстве и времени. В геометрии Минковского в действительном треугольнике обязательно одна из сторон (AB) должна быть больше двух других(AC и CB) (рис. 13). Поскольку в геометрии Минковского интервал между событиями инвариант, то есть, величина, не зависящая от выбора системы отсчета, то и длины сторон произвольного треугольника от выбора системы отсчета не зависят. Поэтому во многих случаях треугольники можно изображать без привязки к определенной системе отсчета. 
На диаграмме Минковского, на евклидовой плоскости, сумма длин двух любых сторон треугольника больше длины третьей стороны. В геометрии Минковского это свойство не выполняется и действует правило: длина наибольшей стороны (AB) действительного треугольника больше суммы длин двух других сторон (AC и CB). Причем, это правило действует для любого действительного треугольника, независимо от его размеров и ориентации в пространстве и времени. Две короткие стороны действительного треугольника, связанные вместе, образуют простейшую действительную последовательную ломаную линию, состоящую из двух сегментов. Любую более сложную действительную последовательную ломаную линию можно получить из действительной последовательной ломаной линии, состоящей из двух сегментов, последовательно замещая отдельные сегменты ломаной линии парами сегментов. При каждом таком замещении, замещаемый сегмент ломаной линии и пара замещающих его сегментов, образуют действительный треугольник, а поэтому, сумма длин пары замещающих сегментов, меньше длины замещаемого сегмента. Из этого следует, что с каждым замещением прямого действительного сегмента на пару прямых действительных сегментов, как это показано на рисунке 14, длина действительной последовательной ломаной линии в пространстве Минковского будет уменьшаться, хотя на евклидовой плоскости такая операция приводит к росту длины ломаной линии. 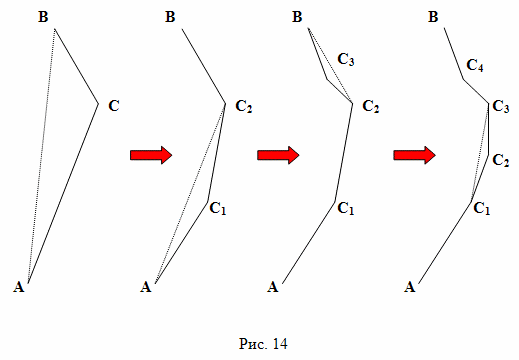
На пределе, мы можем заменить любую действительную последовательную ломаную линию бесконечным числом бесконечно коротких сегментов и таким образом, получить действительную последовательную кривую линию. Продолжая приведенное выше рассуждение, можно установить, что длина любой действительной последовательной кривой линии меньше, чем расстояние между ее началом и ее концом (рис 15). 
Физическая интерпретация действительной последовательной кривой AB, это мировая линия объекта, который движется ускоренно из события A в событие B. А длина этой линии соответствует собственному времени объекта, прошедшее между событиями A и B. И, по законам геометрии Минковского, раз длина этой кривой меньше расстояния между ее началом и концом, то и интервал собственного времени объекта, двигавшегося ускоренно от события A до события B, будет меньше, чем интервал собственного времени объекта, который двигался из события A в событие B прямолинейно и неускоренно. И здесь мне придется огорчить людей, где-то слышавших о том, что ускорение само по себе вызывает замедление хода времени. Общая длина действительной последовательной линии определяется только суммой длин составляющих ее сегментов. Длина действительной последовательной кривой линии тоже определяется суммой длин составляющих ее бесконечно малых прямых сегментов. А из этого следует, что определенное по методу радарной одновременности относительное замедление хода времени ускоренного объекта, относительно инерциального наблюдателя, в каждый момент времени определяется только относительной скоростью объекта. И не нужно путать относительное замедление времени с эффектами, возникающими при повороте системы координат. Но утверждения о замедлении хода времени при ускорении звучали так часто, и делались такими авторитетными людьми, что рассмотрение данного явления нужно проводить отдельно и очень подробно, и это будет сделано несколько позже. Геометрический подход к решению задач теории относительности был бы неполным без определения углов между прямыми линиями, например углов при вершинах треугольников. В евклидовой геометрии есть несколько способов измерения углов, например, один из самых распространенных способов состоит в том, чтобы построить вокруг вершины угла окружность и разделить ее на 360 градусов, а затем определить, сколько градусов попадает в створ угла. В геометрии Минковского этот способ не подходит, потому что аналог окружности в этой геометрии имеет бесконечно большую длину и, разделив ее на конечное число градусов, мы все равно получим бесконечно большие сегменты угла. Окружность в пространстве Минковского, или гиперокружность, как ее иногда называют, уже была изображена на рисунке 9 в прошлой главе, когда мы рассматривали искажения, возникающие при отображении объектов из пространства Минковского на диаграмму Минковского в евклидовом пространстве. Но, чтобы подчеркнуть то, что это не гипербола, а именно такова окружность в пространстве Минковского, я буду и дальше называть ее просто окружностью. В отличие от евклидовой геометрии, в геометрии Минковского линия окружности не замкнута и при отображении на евклидову плоскость в декартовых координатах выглядит как гипербола. Для того, чтобы использовать эту линию для измерения величин углов необходимо применить другой метод, тот при помощи которого в евклидовой геометрии измеряют углы в радианах. В евклидовой геометрии это выглядит так. Проводится окружность с центром в вершине угла, затем измеряется длина части окружности, попавшей в створ угла. А затем, эта величина делится на длину радиуса вектора, при помощи которого была построена окружность (рис. 16). Полученная величина называется величиной угла в радианах. В этих единицах полный угол 360° будет равен 2π, развернутый угол 180° будет равен π, а прямой угол 90° будет равен π/2. 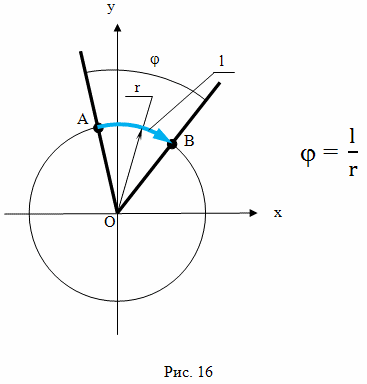
Аналогично и в пространстве Минковского можно использовать окружность для измерений величин углов. Делаем все точно так же, измеряем длину части окружности, попавшей в створ угла, и делим ее на величину радиуса окружности (рис. 17). 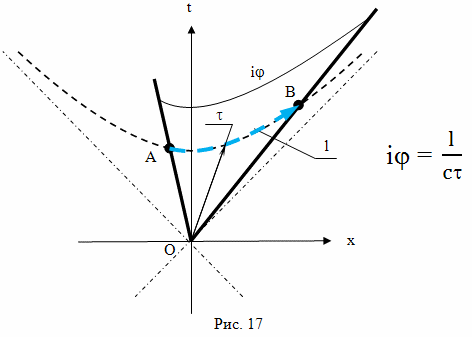
И здесь опять появляются отличия от евклидовой геометрии. В евклидовой геометрии и длина части окружности, попавшей в створ угла, и величина радиуса действительные числа, следовательно, и отношение этих величин действительное число. В геометрии Минковского действительной является величина радиуса, а длина части окружности, попавшей в створ - мнимое число, следовательно, величина угла, измеренного таким способом, тоже будет мнимой величиной. Обозначим ее так: 
В этой формуле мнимая величина l/c - длина участка окружности, попавшей в створ угла , приведенная к единицам времени, а τ - радиус окружности в единицах времени, поскольку эта величина равна собственному времени объекта, который движется инерциально из центра окружности к любому из событий, расположенных на окружности. Теперь можно перейти непосредственно к тригонометрии. В евклидовой геометрии элементарные тригонометрические формулы определяются соотношением длин и величин углов в прямоугольном треугольнике (рис. 18). 
Очень похожие элементарные тригонометрические соотношения верны и в геометрии Минковского на пространственно-временной плоскости (рис. 19). 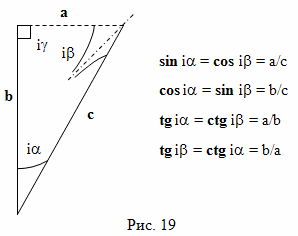
Обратите внимание! В геометрии Минковского, в пространственно-временной плоскости, перпендикуляром действительной прямой может быть только мнимая прямая, а поэтому, прямоугольный треугольник всегда содержит одну действительную сторону (на рисунке 19, это сторона b) и одну мнимую сторону (сторона a), а третья сторона может быть и мнимой, и действительной. Мнимая сторона a показана пунктирной линией. Дуга угла iα на схеме загибается вверх, в соответствии с правилами построения дуги окружности. Угол iβ составной, то есть, он состоит из двух частей, которые разделены световой прямой, обозначенной штрихпунктирной линией. Но здесь возникает чисто технические проблемы, определение величины тригонометрической функции от мнимой величины, а еще, определение величины составного угла. А поэтому, при расчетах используют тождества: 
И теперь, подставляя вместо мнимых чисел iα и iβ, действительные числа α и β, можно определить соотношения в прямоугольном треугольнике, используя гиперболические функции: 
Остается только разобраться с составным углом β, да и прямой угол γ тоже составной. Углы в пространственной области определяются по тому же алгоритму, только в этом случае, радиус-вектор окружности имеет мнимую величину, а длина участка гиперокружности Минковского - действительную (рис. 21). 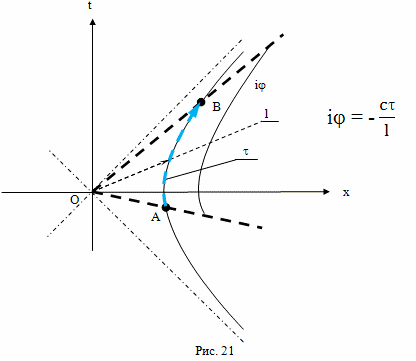
В этом случае, величина угла определяется из отношения длины действительной длины части окружности, попадающей в створ угла к мнимой величине радиус-вектора и она равна: 
Смена знака при значении угла в этой формуле, по сравнению с формулой для временной области, выражается в смене направления обхода угла. Например, если мы принимаем в качестве положительного направления обхода во временной области направление по часовой стрелке, то в пространственной области положительное направление обхода будет против часовой стрелки. Поэтому, для правильного определения величины угла необходимо задавать направление обхода угла при его измерении. На рисунке 22 стрелками показан пример выбора положительного направления обхода угла. Если мы будем измерять угол между двумя прямыми a и b, прямую a зафиксируем, а прямую b будем поворачивать на диаграмме Минковского вокруг вершины угла по часовой стрелке (b0), то величина угла φ будет расти и, по мере приближения к направлению световой линии (c1), будет стремиться к бесконечности. 
Угол между прямой a и ближайшей по часовой стрелке световой линией (c0) будет равен плюс бесконечности. За этой световой линией (b2) направление обхода угла изменится и величина φ начнет уменьшаться. Но при этом, угол приобретет качество, которое не выражается через величину φ и равно целому числу, равному количеству световых линий, попадающих в створ угла. Обозначим это качество через букву d, которую в евклидовой геометрии используют для обозначения прямого угла. Тогда полная запись величины угла может выглядеть например так: 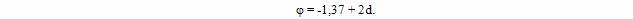
Итак, в промежутке между световыми прямыми c1 и c2, при движении по часовой стрелке, величина монотонно уменьшается и, при приближении к прямой c2 стремится к минус бесконечности (рис. 23). 
В верхней части диаграммы на рисунке 23 показано как изменяется φ - первый параметр угла, при движении по часовой стрелки. В нижней части этой диаграммы показано как изменяется второй параметр nd при пересечении углом световых линий. При таком представлении прямые углы будут равны величине 0±d. Как видно, аналогия с прямым углом евклидовой геометрии не случаен, и в случае геометрии Минковского величину 0±d, в литературе по данному вопросу, принято называть бесконечный прямой угол (см. [19] стр. 178). Развернутый угол будет равен величине 0±2d. В геометрии Минковского сумма углов любого треугольника будет равна 0+2d, то есть развернутому углу, или двум прямым углам. Полный угол будет равен 0±4d. Как видно из рисунков, полный угол состоит из четырех отдельных участков гиперокружности, двух мнимых участков и двух действительных. Параметр d, прямой бесконечный угол, вносит изменения в тригонометрические формулы. При его использовании необходимо использовать следующие тождества: 
И теперь остается добавить еще маленький штрих. В евклидовом пространстве при повороте прямой линии на угол φ (a→a'), перпендикуляр к этой линии поворачивается на угол φ в том же направлении (b→b') (рис. 24). 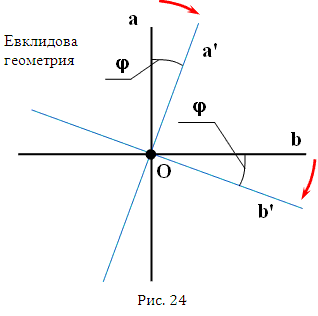
Если мы внимательно рассмотрим приведенную выше методику, то обнаружим, что в геометрии Минковского это свойство тоже отличается от свойства евклидовой геометрии. Если мы в пространстве Минковского повернем любую прямую на угол φ (a→a'), то перпендикулярная ей линия повернется тоже на угол φ, но в другом направлении (b→b'), так, как это показано на рисунке 25. 
При этом, и между прямыми a и b, и между прямыми a' и b', прямой бесконечный угол будет по прежнему равен величине 0+d. Цитируемая литература: [1] Альберт Эйнштейн Собрание научных трудов в четырех томах. Под редакцией И. Е. Таммма, Я. И. Смородинского, В. Г. Кузнецова. Том 1. Работы по теории относительности (1905-1920) Серия: "Классики науки". Изд. "Наука" Москва 1965 г. [2] Альберт Эйнштейн Собрание научных трудов в четырех томах. Под редакцией И. Е. Таммма, Я. И. Смородинского, В. Г. Кузнецова. Том 2. Работы по теории относительности (1921-1955) Серия: "Классики науки". Изд. "Наука" Москва, 1966 г. [3] А. С. Эддингтон "Теория относительности" ОНТИ Государственное технико-теоретическое издательство Ленинград, Москва, 1934г. [4] Макс Борн "Эйнштейновская теория относительности", изд.2-е, испр. Издательство "Мир", Москва, 1972 г. [5] Угаров В. А. "Специальная теория относительности", изд. 2-е, пер. и доп. Издательство "Наука", главная редакция физико-математической литературы, Москва, 1977 г. [6] Окунь Л. Б. "Понятие массы", журнал "Успехи физических наук" Июль 1989 г., стр. 511. Официальный сайт журнала http://ufn.ru/. [7] Бёрке У. (William L. Burke) "Пространство-время, геометрия, космология". Пер. с англ. - Москва: Мир, 1985. [8] Рейхенбах Ганс "Направление времени". Пер. с англ. Изд 2-е стереотипное. - Москва, Едитория УРСС, 2003. [9] Н. А. Черников "Геометрия Лобачевского и релятивистская механика". Физика элементарных частиц и атомного ядра, 1973, том 4, Вып. 3. Объединеный институт ядерных исследований, Дубна. [10] Н. А. Черников "Трудные вопросы теории относительности". Физика элементарных частиц и атомного ядра, 1987, том 18, Вып. 5. Объединенный институт ядерных исследований, Дубна. [11] В. Н. Дубровский, Я. А. Смородинский, Е. Л. Сурков "Релятивистский мир".- М.: Наука, Главная редакция физико-математической литературы, 1984. (Библиотечка "Квант". Выпуск 34. [12] Я. П. Терлецкий "Парадоксы теории относительности". изд.Наука, Москва 1966 г. [13] А. И. Жуков "Введение в теорию относительности". Государственное издательство физико-математической литературы, Москва 1981 г. [14] В. Курганов "Введение в теорию относительности", пер. с франц. В. Д. Захарова. Изд. "Мир", Москва 1968г. [15] Ф. С. Завельский "Масса и ее измерение". М.: Атомиздат, 1974. [16] Эйнштейновский сборник 1974. Ответственные редакторы В. Л. Гинсбург и Г. И. Наан, Составитель У. И. Франкфурт, Акадкмия Наук СССР, Отделение ядерной физики, Москва, Издательство "Наука", 1976 г. [17] Р. Толмен "Относительность термодинамика и космология". Пер с английского. Под ред. Я. А. Смородинского. Изд. Наука, Главная редакция физико-математической литературы, Москва 1974. [18] Л. Д. Ландау Е. М. Лифшиц "Теоретическая физика в десяти томах. Том II. Теория поля". Изд. седьмое, исправленное. Москва, "Наука", Главная редакция физико-математической литературы 1988 г.